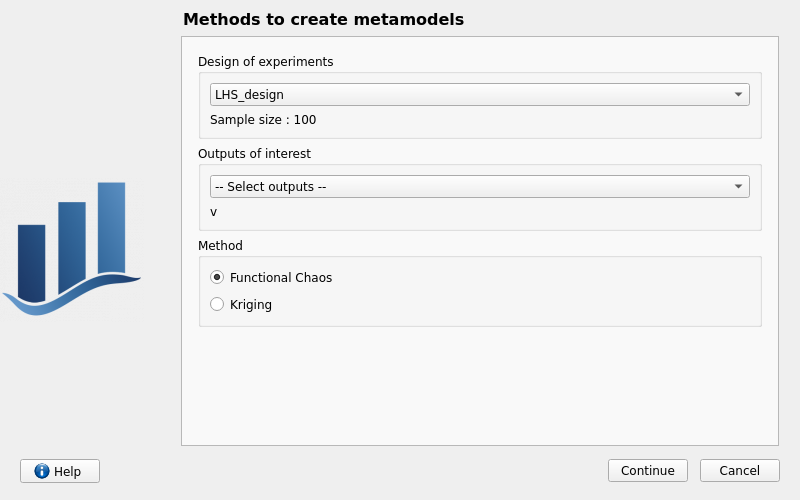
A metamodel is created from a design of experiments established in Persalys or from a data model.
The objective of a metamodel is to replace the initial model, particularly when the latter is very expensive.

Persalys offers two methods:

• linear regression
• polynomial chaos expansion
• Kriging, also known as Gaussian process

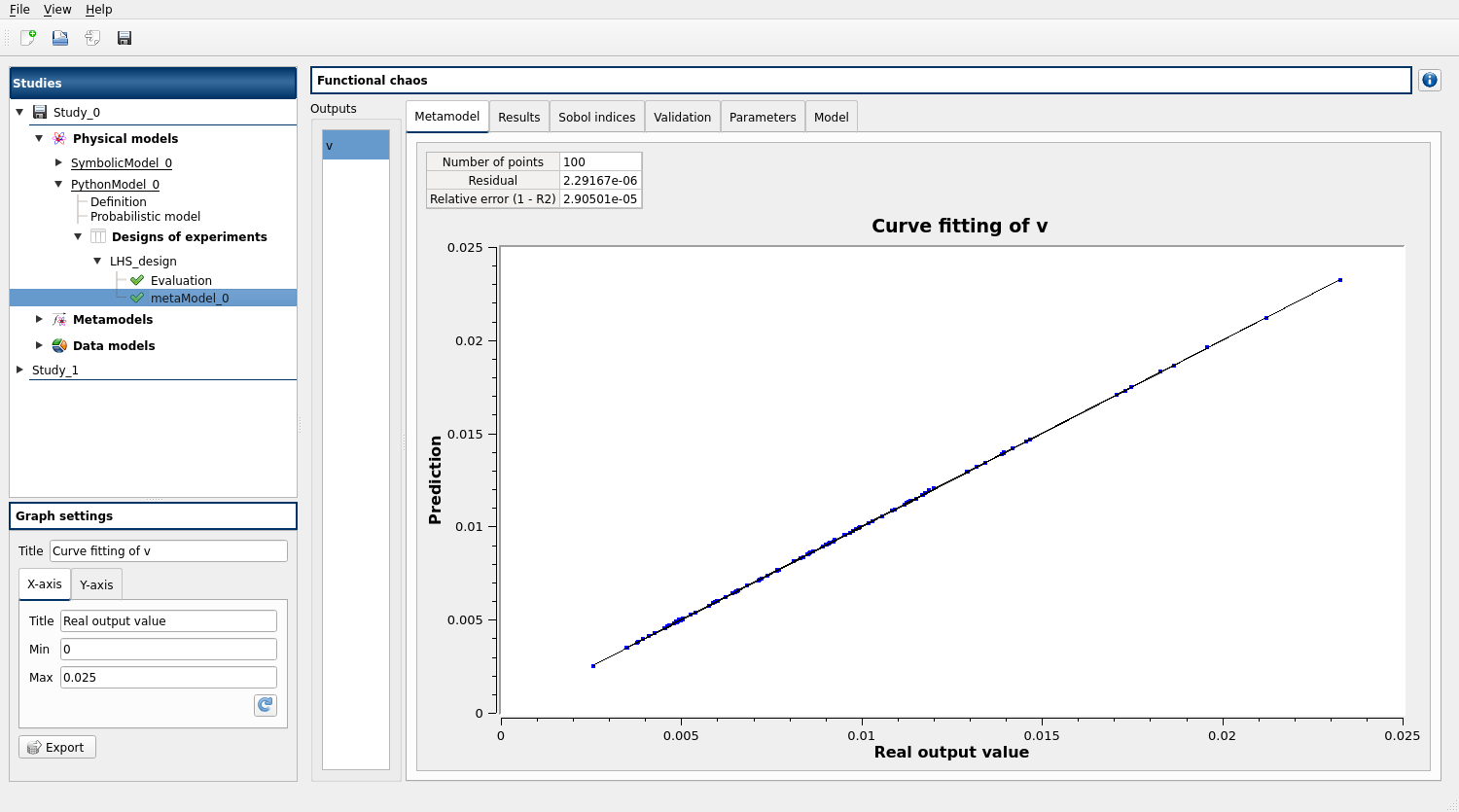
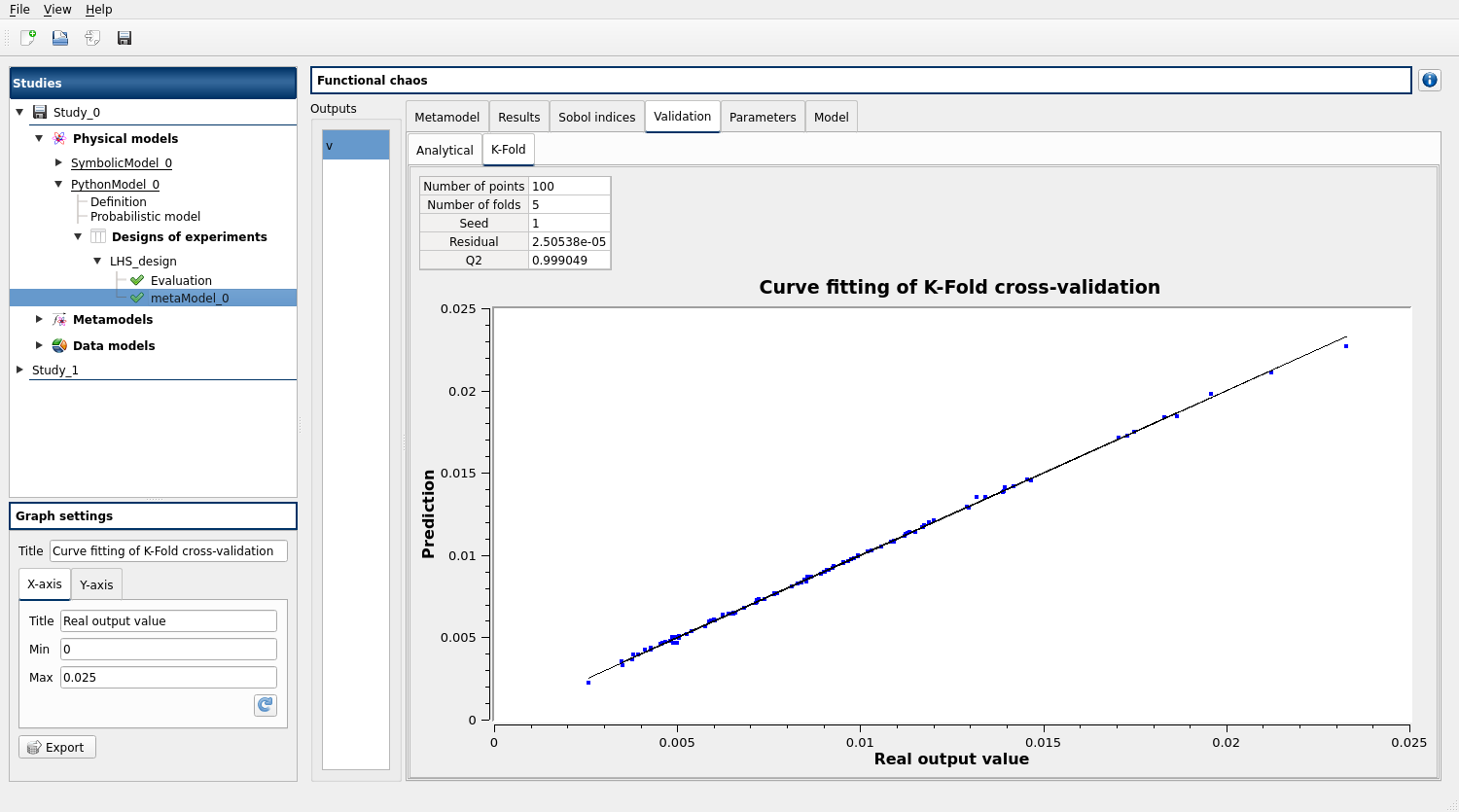
Cross-validation methods included in Persalys make it possible to validate the creation of your metamodel and thus, ensure that it matches the initial model.
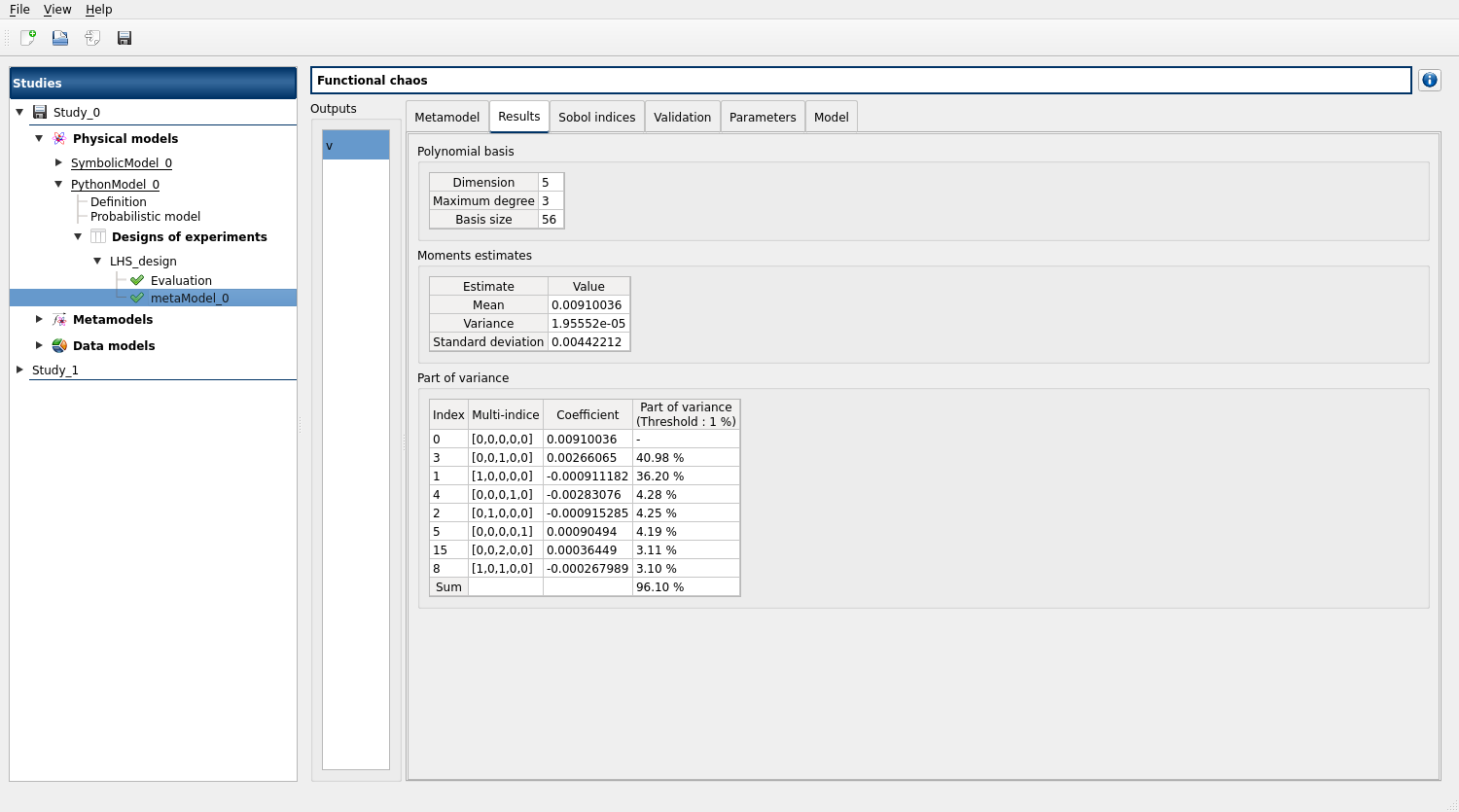
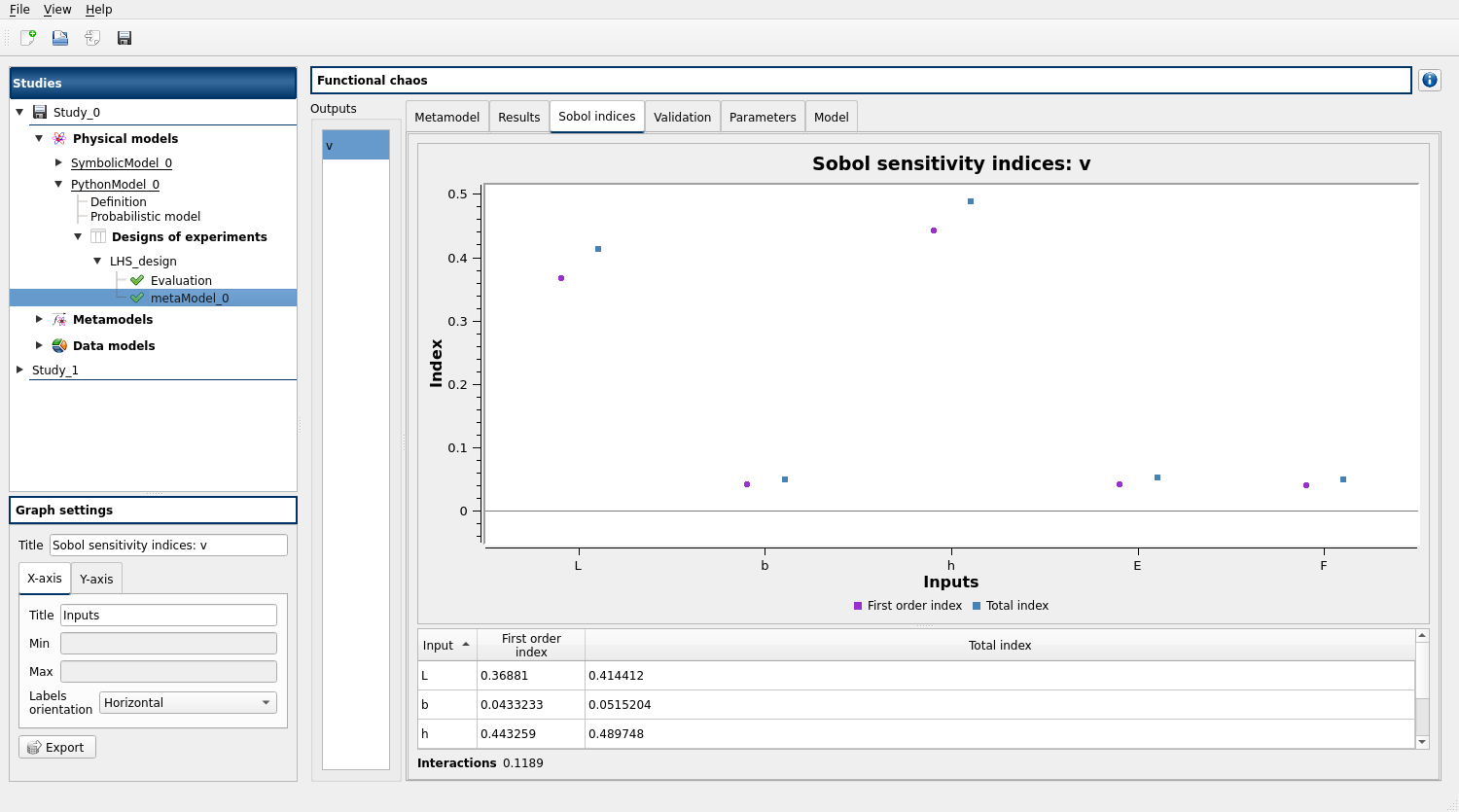
In the case of the polynomial chaos, the Sobol indices are also provided by default.

Once the metamodel is created and validated, you can convert it into a physical model. All the features in Persalys can be applied to it.

For more information on how to create a metamodel, refer to the following video: